Concave and Convex Functions

Intuitively, this can be thought of (in the case where $X\subseteq \mathbb{R}$) as the line segment joining $(x_1,f(x_1))$ and $(x_2,f(x_2))$ being above the function.

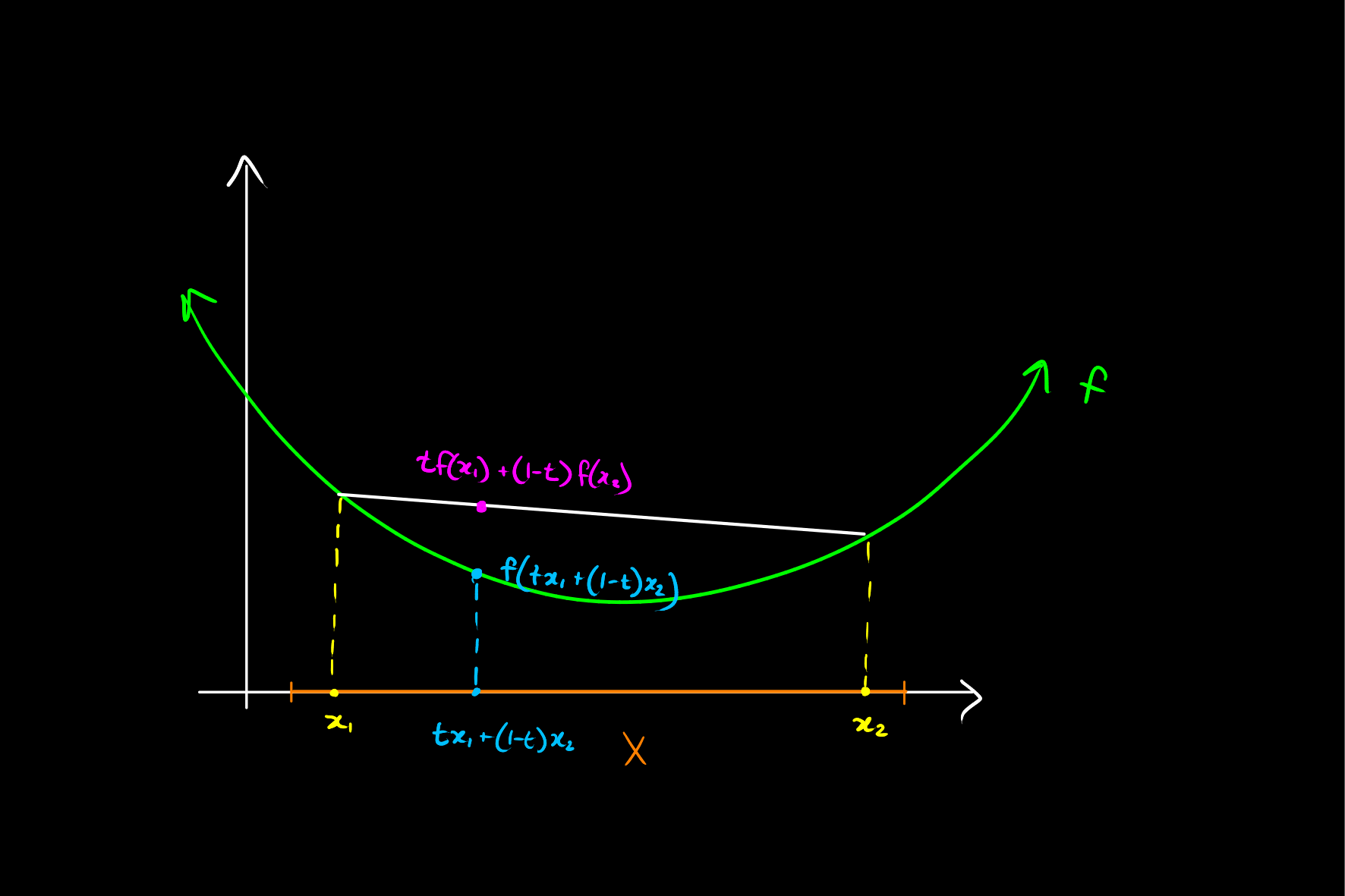
A function is called concave if the above condition is changed with the reverse inequality:

The above conditions are called strict convexity and strict concavity respectively if the inequalities are strict. This is why we use the domain $(0,1)$ for $t$ rather than $[0,1]$ even though the endpoints are trivially satisfied, so that these strict cases are meaningfully defined.

An important corollary of this result gives when the value $f(a+b)$ can be compared to $f(a)+f(b)$ described here.